 The "per bit SNR" is more commonly known as Eb/No, the ratio of the
received energy per data bit, Eb, to the noise spectral density, No. I
will use that term in the rest of this paper.
The "per bit SNR" is more commonly known as Eb/No, the ratio of the
received energy per data bit, Eb, to the noise spectral density, No. I
will use that term in the rest of this paper.
This paper proposes a new transmission format for AO-40 telemetry that uses strong forward error correction (FEC) coding. During fading, this format performs dramatically better than the current uncoded format. Weak-signal performance without fading is also significantly improved. The proposed format can be implemented entirely in software and uploaded to the AO-40 IHU.
The coding methods presented here are not new. They are drawn from deep space telecommunication standards and from direct satellite broadcasting. These methods, and the open-source software modules I have written to implement them, are broadly applicable to other amateur satellite links. The time has come to make FEC a standard feature of every amateur digital satellite link.
This format was a significant improvement over the simple digital communication methods then in use by radio amateurs, such as CW and RTTY. But its only use of error control coding (ECC) is a simple cyclic redundancy check (CRC) that can only detect errors, not correct them.
The Phase 3 format did not use any of the powerful error correction codes that had just been introduced on deep space probes such as Pioneer and Voyager. Although these codes are easy to encode even on a IHU, they were just too complex to decode on the personal computers then available to hams. Dedicated hardware decoders weren't practical either.
The situation has completely changed. Today's personal computer is an extraordinarily powerful digital signal processing (DSP) and encoding/decoding engine. The Pentium/Athlon (PC) and Power PC G4 (Macintosh) CPUs even provide "vector" instructions specifically intended for high performance digital signal processing. Similar instructions were once found only in high-end supercomputers like Crays. Indeed, the average PC now significantly outperforms Cray's early models.
With these advances, it is now fully practical to realize the benefits of FEC on AO-40 and future spacecraft. The primary benefit would be a dramatic improvement in the reliability of AO-40 telemetry when the antennas are off-pointed from earth and spin-induced fading is significant. Even under non-fading conditions, FEC coding would permit the acquisition of AO-40 telemetry with substantially smaller antennas than the uncoded format presently requires. The FEC format would also provide a substantial margin of safety during the commanding of spacecraft maneuvers.
Ground station antennas are often limited in size by practicality and local regulation. Amateurs use the quietest preamplifiers available, despite their high cost, but there are still natural noise sources that cannot be eliminated.
Amateurs have spent a lot of money and effort to maximize the amount of RF power their satellites beam to earth, and to maximize the signal-to-noise ratios of these signals as received at their stations. But two critical elements of the system remain unchanged: modulation and coding.
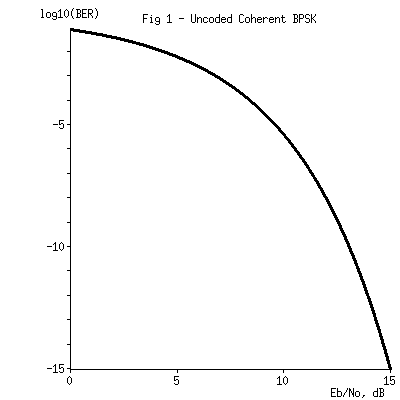
Binary phase shift keying (BPSK), as used by the AO-40 telemetry beacon, is one of the oldest and most widely used modulation schemes in space communications. Figure 1 shows the bit error rate of an ideal BPSK demodulator as a function of the "per-bit" signal-to-noise ratio.
 The "per bit SNR" is more commonly known as Eb/No, the ratio of the
received energy per data bit, Eb, to the noise spectral density, No. I
will use that term in the rest of this paper.
The "per bit SNR" is more commonly known as Eb/No, the ratio of the
received energy per data bit, Eb, to the noise spectral density, No. I
will use that term in the rest of this paper.
This plot makes several important assumptions. First, the demodulator is "coherent"; it recovers the phase of the transmitted carrier from the incoming signal, and it does so perfectly. Second, the only channel impairment is "white" Gaussian noise, such as the thermal noise of a preamp. There is no fading. This is an important point we'll return to later.
According to the Nyquist Theorem, BPSK must occupy a bandwidth of at least 1 Hz for every bit per second of signaling rate. I.e., its "spectral efficiency" is 1 bit/sec/Hz. And according to the Shannon Channel Capacity Theorem, there exists a signalling scheme with a spectral efficiency of 1 bit/sec/Hz that can achieve error-free performance provided that the Eb/No is at least 0 dB. (No such scheme exists that requires an Eb/No of less than 0 dB.)
As you can see, achieving a good error rate with uncoded coherent
BPSK, even with a perfect demodulator, needs about 10 dB more power
than the Shannon limit requires. How can we make up at least some of
the difference? With forward error correction coding. The power
we can save with a given FEC scheme over uncoded BPSK is
the coding gain.
On a fading channel, the case for coding is even more dramatic. The Rayleigh fading model is commonly used, as it accurately models propagation over multiple, time-varying reflected paths. EME and HF skywave are well modeled by Rayleigh fading. The Ricean model generalizes the Rayleigh model by adding a direct free-space path to the indirect multipath components. Land mobile channels are often modeled as Ricean.
Except for satellites on HF, most amateur satellite link fading is
caused entirely by satellite spin or tumbling combined with nonuniform
antenna patterns. This is the case when AO-40's antenna is off-pointed
from earth. The fading envelope repeats predictably on every rotation,
and depending on spacecraft attitude, the envelope can include one or
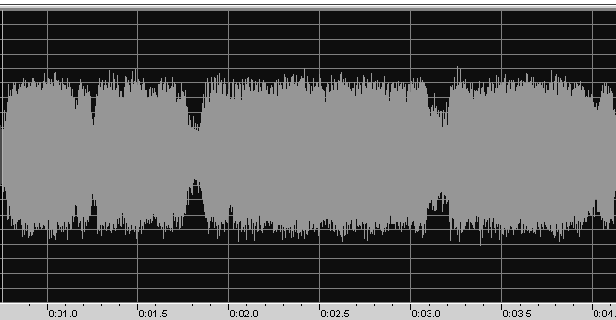
more deep nulls. Here is an amplitude plot of AO-40 S-band telemetry
as received by W2GPS and WB4APR using the 12-meter dish at the US
Naval Academy on January 18, 2001. The time span is 3.38 seconds, the
spin period at that time. The receiver AGC could not be turned off,
so the fading was even more severe than shown here:
Without FEC, a telemetry frame is no stronger than its weakest bit. A short, deep fade that causes a single bit error is enough to destroy an entire frame even if the average Eb/No is high. Because a frame is about 11 seconds long and there can be multiple deep fades per satellite rotation when the antennas are not earth-pointing, every frame is almost guaranteed to have at least one bit error. With FEC, however, the bits corrupted in a fade can be regenerated from the others that are received. It doesn't matter how deep the fades are, as long as most of the frame gets through.
So the coding gain that FEC can achieve on a fading channel depends
on the fade depth. FEC that can "ride through" say, a 30 dB fade, can
provide a coding gain of 30 dB over and above that provided on a
non-fading channel. We amateurs can no longer afford to ignore such
dramatic gains!
A complete review of all FEC codes would fill a large textbook, so I'll limit my discussion to the code I'm proposing for use on AO-40. This is the concatenated Reed-Solomon/Convolutional code first flown on Voyager 1 and 2 in 1977, and now widely used in very similar form by every major digital broadcast satellite.
A "concatenated" code is formed by combining two separate codes, in this case a Reed-Solomon block code and a "short" convolutional code decoded with the Viterbi algorithm. (One sometimes hears the term "Viterbi code", but this is inaccurate. Viterbi's contribution was an efficient algorithm for decoding convolutional codes, which were already known at the time.)
Here is a communications system that uses a concatenated code:
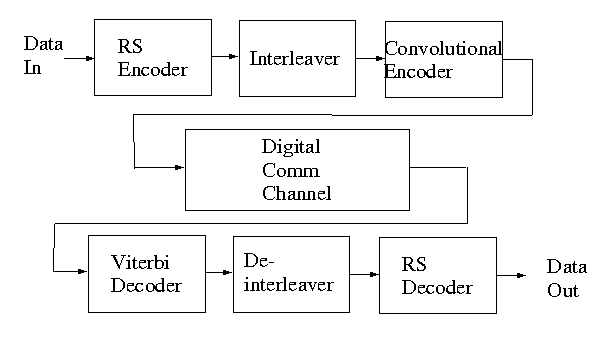
The user data is first encoded with a Reed-Solomon code. The Reed-Solomon data is interleaved (reordered) and encoded again, this time with a convolutional code. At the receiver, the convolutional code is decoded with a Viterbi decoder, the data is de-interleaved and the Reed-Solomon code is decoded.
In this scheme the Reed-Solomon code is sometimes referred to as an "outer code", while the convolutional code is an "inner code". Why use two codes? And why the interleaver? To get the best of both kinds of codes.
Viterbi-decoded convolutional codes provide excellent coding gain on Gaussian channels with random channel bit errors, and they are readily adapted to soft decision decoding. If the demodulator can provide a "quality" indication with each incoming bit, the Viterbi algorithm yields an extra coding gain of about 2 dB over that from a demodulator with a simple slicer at its output. Typically 3- or 4-bit samples are used.
The Viterbi-decoded convolutional code first used on Voyager has
become very widely used. It is a Consultative Committee for Space
Data Systems (CCSDS) standard. Here is a block diagram of the
encoder:
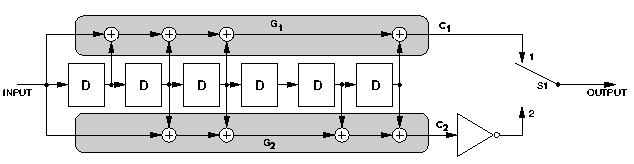
This particular code has a constraint length of 7
and a rate of 1/2. That is, there are taps at 7 points
along the encoder shift register,
and it generates two encoded channel symbols for each
input data bit.
A description of the Viterbi algorithm is beyond the scope of this
paper, but its performance on this code on a coherent BPSK channel
with 3-bit soft decision symbols is shown here:
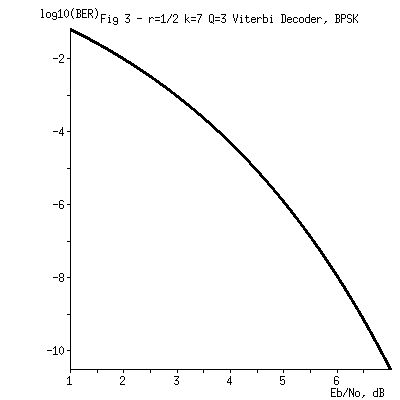
Note the improvement over uncoded BPSK. To achieve a bit error rate of 10^-5, the coded channel requires an Eb/No of about 4.5 dB. That's 5.1 dB less than uncoded BPSK. In other words, just by using this code you can cut your transmitter power by a factor of 3.2 and keep the same user data rate. Or you could increase your data rate by that same factor of 3.2 while keeping the same transmitter power, ground antenna, etc.
This does come at the cost of doubling the channel bandwidth, as the encoder generates two channel symbols for each data bit.
A Viterbi decoder still makes errors, and it cannot reliably tell you where they are. A telemetry system needs protection against these errors, so we need something else on top of the Viterbi-decoded convolutional coding.
One could just use a CRC, and some systems (e.g., IS-95 CDMA digital cellular) do just that. But if our data blocks are large enough, we can do better with a more powerful code.
Reed-Solomon (RS) codes are well known for their use in CDs and CD-ROMs. They are "block" codes like CRCs, only much more powerful. The RS code in my proposal is also a CCSDS standard, similar to Voyager's (255,223) RS code. Each code block contains 255 8-bit symbols. 223 symbols contain user data and 32 symbols contain parity computed according to the code specification.
A (255,223) RS code not only provides extremely reliable error detection, it can also correct up to (255-223)/2 = 16 symbol errors in each block. At least one bad bit in a symbol spoils the whole symbol; it doesn't matter if the other bits are also bad. This makes RS codes better suited to the correction of burst errors than random errors.
It turns out that Viterbi decoders always make their errors in bursts. This makes for an ideal marriage between a Reed-Solomon code and a Viterbi-decoded convolutional code. The Viterbi decoder does most of the work, and the RS decoder "mops up" most of the remaining errors. Any uncorrectable errors that remain are almost guaranteed to be detected.
When these two codes are combined, the BER curve is a nearly vertical cliff at an Eb/No of about 2.5-2.6 dB.
Here is a block diagram of the complete frame encoder for AO-40.
Besides the Reed-Solomon and convolutional encoders and the interleaver
between them, several more components are included: a scrambler that
ensures frequent symbol transitions regardless of the input data, and
a second interleaver.
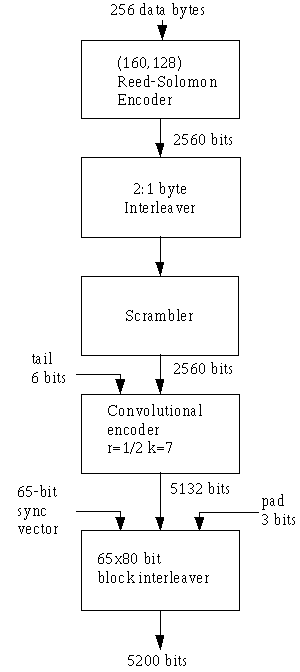
The current, uncoded Phase 3 telemetry frame has a data payload of 512 bytes. Early in the project, it was decided that a payload of only 256 bytes would be acceptable in the FEC format. This reduces the IHU RAM needed to build the encoded frame, and it keeps the frame from taking too long to transmit at the fixed rate of 400 bps.
The 256 bytes of telemetry data are divided into two blocks of 128 bytes each. Each block is zero-padded at the start with 95 bytes of binary zeros to make 223 bytes of data for the Reed-Solomon encoder. This zero-padding is reinserted at the decoder; it is not sent over the air. This shortening process effectively turns the original (255,223) code into a (160,128) code. Each block still has 32 parity symbols and can still correct up to 16 symbol errors. Because fewer symbols are actually transmitted over the air, the percentage of symbols that can be in error is increased, strengthening the code at the expense of greater overhead.
The 320 bytes of RS-encoded data are interleaved, scrambled and fed to the k=7 r=1/2 convolutional encoder. A "tail" of six 0-bits is added to the end of the scrambled frame to return the convolutional encoder to the all-zeros state.
Because fade-resistance is a specific goal, a second layer of interleaving -- unique to the AO-40 format -- was added after the convolutional encoder, just before the modulator. This is necessary because Viterbi decoders do not do well on fading channels. It was not needed on Voyager because that spacecraft is 3-axis stabilized and does not suffer from the kind of spin fading that affects AO-40.
For the same reason, the existing Phase 3 block sync vector scheme could not be used. A "distributed" sync vector, 65 bits long, is interleaved with the data so that a single fade at the wrong moment cannot kill the entire frame.
Each coded frame contains exactly 5200 encoded bits (binary channel symbols) and takes exactly 13 seconds to transmit at 400 bps. The user data payload is 256 bytes, or 2048 bits. The remaining 5200 - 2048 = 3152 channel symbols contain FEC overhead, a sync vector, and a few spare bits.
A more detailed description of the format, and the
rationale for each design decision, is in my paper, Proposed Coded AO-40
Telemetry Format.
The answer is to use differentially coherent demodulation (DBPSK). A coherent detector extracts its carrier phase reference from a relatively wide sliding window of received symbols, but this window is a big target for a channel phase disturbance. DBPSK only uses the phase of the symbol immediately before the one we're demodulating, so a short disturbance only affects a few symbols.
For DBPSK to work, we must specially encode the data at the transmitter. I.e., we want to encode a 1-bit not as a particular carrier phase, but as a change of phase from one symbol to the next. Similarly, a 0-bit is encoded as no phase change. That allows us to recover the data by directly comparing pairs of received symbols.
Fortunately, AO-40 already does this. The IHU includes a hardware differential encoder and a Manchester (biphase) encoder. If a 1-bit is to be sent, the 400 Hz beacon clock is inverted in phase from its previous setting; if a 0-bit is to be sent, the beacon clock phase is left unchanged. Bits thus encoded are then fed to the BPSK beacon modulator and to the transmitter.
DBPSK can be demodulated in software as follows. We take the digitized audio signal from the receiver and feed it to a complex (I&Q) mixer and low-pass filter. The mixer "local oscillator" is set close to the incoming carrier frequency. This produces a complex baseband signal with a carrier frequency close to zero hertz. (This is commonly known as a "zero IF" conversion.)
Because the LO is not locked to the carrier, the zero-IF signal
vector will slowly rotate in phase. The closer the LO is to the
carrier frequency, the slower the vector rotation. At the same time,
the vector will flip 180 degrees and return according to the
modulation.
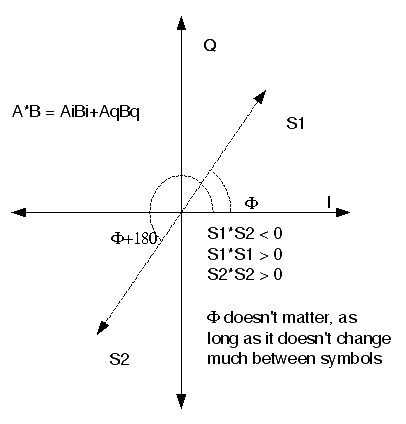
To extract the modulation, we compute the vector dot product of the complex baseband signal samples for the previous and current channel symbols. If there has been no change in phase between the two symbols, the dot product will be a positive number. If the phase has changed, the dot product will be negative. The magnitude of the dot product depends on the vector magnitude of both symbols; if the symbols are weak, the dot product will be small. We just flip the sign on each dot product, and we have our soft-decision values for our Viterbi decoder!
There's a little more to the problem. We have to know where each symbol starts and ends, and we also need to know the approximate incoming carrier frequency so that the zero IF signal vector won't drift too much between each pair of symbols (not counting the modulation, of course).
Given the power of the modern PC, simple brute force works well here. I start by simply trying all possible combinations of carrier frequency and symbol timing, looking for maximum demodulator output. But I need not do this on every frame. Carrier frequency and subcarrier phase usually don't change much from one telemetry frame to the next, so I can simply use the values acquired for one frame as initial guesses for the next. If the guess is right, the frame decodes. If not, I can drop back and retry the frame with the brute-force search.
All this is still a lot easier to implement than coherent BPSK (CBPSK) demodulation with a Costas or squaring loop. And while DBPSK works well on channels with rapid carrier phase disturbances, CBPSK often fails completely.
But DBPSK has its price. On a non-fading channel, CBPSK outperforms DBPSK. A coherent detector produces a carrier phase reference from the energy of many channel symbols, while the DBPSK demodulator can use only the energy of one symbol as a reference.
At high Es/No ratios, such as those required for uncoded PSK, the advantage of CBPSK over DPSK is only a small fraction of a dB. (Es/No is the signal-to-noise ratio seen by the demodulator rather than the FEC decoder. In an uncoded system, a channel symbol and a data bit are the same thing, so Es/No = Eb/No. We've seen that this has to be about +10 dB for uncoded BPSK). This raises the question of why so many Phase 3 BPSK demodulators use coherent detection despite the increased complexity and difficulty in use.
But in a FEC-coded system, the Es/No is the Eb/No times the code rate: about 0.4, or -4 dB in the present scheme). Thanks to the FEC coding gain, we can operate at a much lower Eb/No of about 2.6 dB, and the Es/No is another 4 dB below that, or about -1.4 dB. That's low enough for the DBPSK penalty to become significant.
I have tested my prototype demodulator on simulated channels with Gaussian (thermal) noise and with and without fading. Both NRZI and Manchester symbol filtering were tested, although only Manchester is compatible with the AO-40 IHU. (More on this later).
In this case, 100% copy is achieved at Eb/No >= 8 dB, but only about 10% of the frames are decoded at Eb/No = 7 dB. In this particular situation, the addition of fading results in about a 2 dB impairment.
Solid copy is achieved at Eb/No >= 7 dB, and 50% copy at Eb/No = 6 dB. This is about 1 dB worse than with NRZI. This is due to inter-symbol interference in the transmit filter that is unequalized in the receiver. A receive equalizer should remove most of this penalty, but some may remain.
The FEC format's fade tolerance depends on fades being brief relative to the 13 sec frame time. Tests do show worse performance on very long fade periods, as expected. This could be improved with a longer interleaver, but only at the expense of increasing the delay between the generation of a frame by the IHU and its decoding on the ground. So 13 seconds was chosen as an initial compromise. If experience shows that a longer interleaver would be desirable, the format can be changed.
On a fading channel, we have no choice but to use differentially coherent (DBPSK) demodulation. But I could improve the performance of my demodulator under non-fading conditions by adding a CBPSK demodulator. DBPSK could be tried first, and it will succeed if the signal is strong enough. If not, the CBPSK demodulator could then be tried automatically.
Another possible enhancement is suggested by the technique developed by Paul Willmott, VP9MU, to merge AO-40 telemetry fragments from multiple stations. This recovers data that might not be available from any one station. This approach is even more powerful when FEC coding is in use, and it is routinely performed on signals from the Galileo spacecraft orbiting Jupiter. An array of antennas and receivers is pointed at the spacecraft, and the separate signals are synchronized and combined before demodulation and decoding.
The prototype package uses a set of general-purpose DSP and FEC libraries that can easily be reused in other projects: