
ARISSat-1 will carry a new telemetry modulation and coding scheme, BPSK1000, designed to handle the severe fading often encountered with low orbit satellites without attitude control. Its performance and the link budgets for the ARISSat-1 spacecraft are such that reliable reception should require only a simple whip or ground plane antenna, a conventional 2m SSB receiver, and a reasonably modern personal computer with audio A/D input.
BPSK1000 uses differential binary phase shift keying (DBPSK) at a channel symbol rate of 1 kHz in a SSB bandwidth. With constraint length 7, rate ½ forward error correction (FEC), the user data rate is about 500 bits/sec. HDLC framing provides application flexibility (including the ability to carry AX.25 in other applications) and a deep (16 second) convolutional interleaver provides strong protection against fading.
I hope that the demonstrated performance of BPSK1000 on ARISSat-1 will encourage other amateur satellite projects with similar needs to consider it; at the very least, I hope to convince other satellite designers that forward error correction (FEC) should be a standard feature of every amateur satellite data link!
Software to demodulate and decode the ARISSat-1 BPSK1000 beacon will be available for Microsoft Windows, Mac OSX and Linux. I wrote the reference BPSK1000 demodulator and decoder in C under Mac OSX and Linux as libraries and command line tools and I am distributing them under the terms of the GNU General Public License (GPL). I strongly encourage everyone to study, modify, enhance, test, break, fix, improve, experiment with and use what I have written.
My reference decoder is incorporated into the Windows program by Doug Quagliana KA2UPW and the Mac OSX program by Gilbert Mackall N3RZN, both of whom have turned a set of command line tools into complete, user-friendly applications.
My software can use, but does not require, multiple CPUs and the Altivec (Power PC) or SSE (Intel/AMD) vector instruction sets to improve performance, in some cases rather dramatically. Multiple CPUs are used through the POSIX Threads (pthreads) library, and vector instructions are invoked with gcc C complier intrinsics; there is no actual assembly code.
The rest of this paper discusses the physical layer modulation, interleaving, coding, and framing elements of the generic BPSK1000 air interface. Its specific use by ARISSat-1 is documented separately.
Since classroom educational demonstrations are a prime goal of ARISSat-1, my goal was to design a signal format that, while as robust and efficient as possible, should not require any special hardware beyond a general purpose personal computer and a 2-meter receiver or transceiver. Nor should it require any special knowledge, training or practice beyond ordinary ham radio skills. I especially did not want to assume that the operator was already an experienced amateur satellite operator. I want to make it possible for any ham with the necessary equipment, not necessarily one already familiar with amateur satellites, to do a successful classroom demonstration. My hope is that this may entice more kids to become hams, and more hams to join AMSAT.
No one gave me a formal list of requirements beyond "it must work" and "we must have it before such and such date", so I made my own:
Additionally, it should be possible to reliably receive ARISSat-1 telemetry with a small and simple antenna such as an ordinary whip or ground plane. Steered directional antennas should not be required.
Although it would be nice to work with FM-only transceivers, FM is just too inefficient for satellite use. Implementing an efficient modulation mode in software requires a linear transceiver, and that currently means SSB. This leads to the requirement that the signal fit within the typical SSB voice filter response of 300 to 2700 Hz, a bandwidth of 2400 Hz.
A prime personal goal of this project -- as with my previous effort that put an experimental FEC format on AO-40 -- is to demonstrate that there exist far more power-efficient modulation and coding methods for amateur satellite telemetry links than are generally flown. Such improvements can either cut the cost of constructing a satellite by reducing the amount of DC power it must generate, and/or it can make amateur satellites accessible to more hams by reducing the size, cost and complexity of the ground antennas. Many hams live in homes with antenna restrictions where the traditional 2m/70cm yagi combination simply isn't an option.
The AFSK/FM mode used by terrestrial amateur packet radio is particularly inefficient. Quite frankly I am at a loss to understand why anyone would fly it on a spacecraft.
Because forward error correction (FEC) codes can provide a significant "coding gain" that reduces the transmitted energy per bit, this requirement alone dictates the use of FEC, even without the additional dramatic improvements it provides in fading (see below). It has long been easy to achieve coding gains of up to 7 dB on channels impaired by only Gaussian (thermal) noise, and the latest codes can provide gains of up to about 10 dB.
This requirement is closely related to #2 because an inefficient link (i.e., one without FEC) requires a lot of excess power to ride through a fade. An alternative is to keep retransmitting until the data gets through, but all those unsuccessful transmissions are also wasted energy. Fading represents errors that can be corrected by FEC, but not all FEC codes can tolerate the long bursts of errors associated with slow fading. Therefore, we need either FEC suited for burst error correction or an interleaver to break up error bursts into a long series of single bit errors that can be corrected more easily.
To see the huge benefit of FEC on fading channels, consider that without coding you need enough link margin -- excess transmitter power -- to ride through the usual fades. I.e., it must be designed for the worst case. Since the channel is faded for only a small fraction of the time, most of the time all that excess power goes to waste. On the other hand, a well designed FEC scheme for a fading channel will operate as long as the average signal-to-noise ratio is high enough; brief fades, even when infinitely deep, can be reconstructed by the decoder from redundant information received when the channel is not faded. This difference between average and worst case SNR becomes the effective coding gain of the FEC. When the fades become very deep, the coding gains can become truly dramatic. The link simply won't work without it.
I probably spent more time thinking about how best to meet this requirement than all the others combined. The problem is that efficient digital modes tend to sound like band limited white noise, and white noise is notoriously hard to tune to an exact frequency! [1]
Fortunately, an elegant and effective solution presented itself. The ARISSat-1 downlink also includes a CW beacon and I recommended that it simply be moved to the lower null of the digital telemetry signal. Here it will not interfere with the beacon and vice versa, but it can easily be heard and tuned by a human operator in such a way that it automatically tunes the telemetry signal as well.
The only element of signal generation that created any concerns was the BPSK modulation. Not the modulation per se, but the filtering associated with it. The FIR filter is 454 taps long, but not every tap needs to be computed on every sample. By signaling with impulses, most of the delay line will contain zeros, allowing those multiplications to be skipped.
Fortunately, generating BPSK1000 is relatively simple -- certainly far simpler than demodulating and decoding it!
BPSK1000 encoding can be succinctly described as follows:
These elements are all "off the shelf", well documented in the textbooks and used commercially for many years. What follows is a more detailed description and my rationale for selecting each one for this project.
One of the best known and most widely used methods of variable length framing on synchronous bitstreams is HDLC, familiar to most hams from its use in the AX.25 packet radio protocol. Stripped to its bare essentials, this is what an HDLC frame in BPSK1000 looks like:

The special 'flag' sequence 01111110 represents the end of one frame and the start of another. (Two frames may share a common flag, or there may be extra flags between frames; the decoder will work either way.) As called for in the HDLC standard, user data is transmitted least-significant-bit first between the opening flag and the CRC.
To ensure transparency, the HDLC encoder inserts a '0' bit whenever five contiguous '1' bits occur in the data stream. When the receiver sees five '1' bits followed by a '0', it automatically removes the '0'. Although bit stuffing can consume up to 16.7% of the channel capacity in overhead, this occurs only for a data stream of all 1's. The overhead for bit stuffing on random data is much less.
I made only one significant change to standard HDLC framing as used in BPSK1000: I replaced the usual 16-bit CRC with a 32-bit CRC with the generator polynomial: [2]
x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1.
The stronger CRC greatly reduces the chance that a random bit stream will decode as a valid frame.
BPSK1000 treats the contents of the "Data" field as opaque, i.e., it does not care about their contents. Although ARISSat-1 doesn't send AX.25 headers, nothing prevents another BPSK1000 application from doing so. I.e., BPSK1000 could easily carry standard AX.25 packet radio data, although for reasons discussed later it is not well suited to the half duplex, shared channel mode of operation of most amateur packet radio channels.
The fact that BPSK1000 does not assume the presence of AX.25 headers is one reason I decided to enlarge the CRC. Spurious HDLC frames are common in packet radio but they are easy to detect by their absence of an AX.25 header. Because I did not want to make any assumptions about the contents of ARISSat-1 HDLC frames, I chose a longer CRC that all but eliminates spurious frames in the first place.
In sum, HDLC converts an asynchronous stream of arbitrary length frames into a continuous 500 bps bit stream for the FEC encoder. If there's nothing to send, the HDLC encoder must emit an idle flag stream. The HDLC decoder at the receiver regenerates the original series of frames with the 32-bit CRC providing strong error detection. Although BPSK1000 includes forward error correction (FEC), the HDLC CRC is necessary because a Viterbi decoder still makes errors when its error correction ability is exceeded and it cannot reliably signal when they occur.
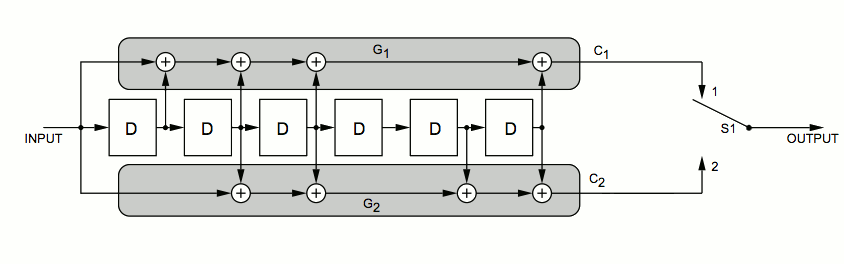
For each data bit from the HDLC encoder, the convolutional encoder generates two symbols, C1 and then C2. I use the CCSDS convention for the ordering of the two encoded symbols but I do not invert either symbol.
The CCSDS and JPL versions of this encoder both invert the output of the 133 (octal) XOR ladder (shown here as symbol C2). Their reason for doing so is to limit the maximum possible number of contiguous 0's or 1's that can come out of the encoder regardless of the data so as to guarantee a minimum symbol transition density for demodulator tracking. That is unnecessary here because HDLC bit-stuffing ensures that no more than five consecutive '1' bits can ever occur in user data, and an HDLC flag consists of six consecutive '1' bits. An HDLC abort, if ever generated, need (and should) consist of only seven '1' bits, followed by an idle flag stream until more data is available for transmission. [4]
Although HDLC does not limit runs of '0' bits, this is not necessary here because of the use of differential encoding before BPSK modulation that turns every '0' bit into a 180° carrier phase transition. It is only necessary to break up consecutive '1' bits as differential encoding sends them as no change in carrier phase.
Interleaving scatters the encoded symbols in time before transmission and rearranges them into their original sequence at the receiver before decoding. This has the effect of breaking up a burst of errors into a much longer sequence of single bit errors that are much more easily corrected.
There are two major classes of interleavers: block and convolutional. Block interleaving is straightforward: the encoded symbols are written into an array by rows and read out by columns for transmission. The receiver reverses the process by writing the array by columns and reading it out by rows.
Delay can be a problem with block interleaving, especially when a large block is required to tolerate deep fades. Nearly the entire block has to be written before transmission can start, and then the entire block has to be received before decoding can even begin. Block interleaving usually requires that a single block size be selected in advance, though some systems use several sizes. However, this doesn't necessarily restrict the system to a fixed data frame size; HDLC or something similar could support variable length data frames just as it does here.
These drawbacks are not necessarily serious. For example, in its FEC mode the AO-40 IHU generated fixed sized 256-byte data blocks more or less instantly, so the delay from block generation in software to the decoded block being available on the ground was equal to just one block transmission time (13 sec) plus the times needed for the IHU to encode it and the ground CPU to decode it.
But when the source is a steady bit stream, or a series of small data frames spread out in time, the encoder must wait for the interleaver block to fill before it can even begin to transmit it. The last data frame in the block will not see any difference, but this can nearly double the time between the generation of the first (small) data frame in the block and when it is available on the ground. [6]
An alternative to block interleaving is convolutional interleaving, [5] and I chose it for BPSK1000 to help reduce latency when small HDLC frames are carried. Just as a convolutional encoder differs from a block encoder by operating on a continuous data stream rather than fixed-sized blocks, a convolutional interleaver also operates on a continuous stream. This is well suited to the continuous stream of encoded symbols from the convolutional encoder.
Here is a block diagram of a small (order 4) convolutional interleaver:

The symbol stream to be transmitted is fed in on the left to the 1:4 rotary switch that deposits each symbol in turn into one of four delay lines whose lengths range from 0 in the first row (no delay) to 3 time units in the last row. Their outputs are collected by the 4:1 rotary switch operating synchronously with the input switch. The delay lines clock only when selected by the rotary switches, which operate synchronously, and the output of the right hand rotary switch goes to the transmitter.
At the receiver, the incoming symbol stream passes through the deinterleaver, the mirror image of the interleaver:

The essential feature of convolutional interleaving is that in each row, the length of the interleaver delay line plus the length of the deinterleaver delay line is a constant, N. In this example, N = 3. So the overall effect of the interleaver and deinterleaver combined is to reproduce the original input stream, in its original sequence, delayed by a number of time units equal to N times the number of rows R; in this example, that would be 12 time units.
N can actually be any number you choose, though it can't be less than R-1 if each row is to have a delay on each side of the channel different from all the other rows. Otherwise some input symbols will be sent in their original order, and that defeats the point of interleaving. And if you make N bigger than this, you're just adding unnecessary delay. So for all practical purposes, N = R-1.
The main advantage of convolutional interleaving over block interleaving is that less memory and less end-to-end delay are required for a given amount of fade protection. One can think of convolutional interleaving as being something like block interleaving but with a single block split between transmitter and receiver.
Convolutional interleaving also has its drawbacks. Because there's no well defined start or finish to the data stream as in block interleaving, it is not well suited to short bursty transmissions like those on a shared, multiple access channel (e.g., conventional packet radio). Conversely, a system that uses block interleaving could key up, send a single block and stop transmitting without having to allow any time to "prime" the de-interleaver or to flush the interleaver.
But that doesn't matter for our application because it's a one-way continuous broadcast. The ground station will still need to prime its de-interleaver at the beginning of the pass. At first this might seem a disadvantage relative to block interleaving, but it's not. Satellite AOS can occur at any time, and were it to occur in the middle of a block in a block-interleaved system you'd have to wait up to one block time for the first full block to start. With convolutional interleaving, priming of the de-interleaver takes the same amount of time no matter when you start.
This got me thinking about playing with some alternative orderings. One common trick in block interleaving is to access the rows and columns in "bit reversed" order. Take the integers from 0-7 and write them in binary:
000, 001, 010, 011, 100, 101, 110, 111
Now reverse them left-right and convert back to decimal:
0, 4, 2, 6, 1, 5, 3, 7
Now access the rows or columns in that permuted order.
Why do this? Well, it helps to spread out adjacent input symbols during an error burst (e.g., a fade). The first errored symbols in the burst are as far apart as they can get in the memory available. Additional errors are evenly sprinkled between the previous errors, though of course if the burst lasts long enough it will eventually have to fill in all the gaps and decoding failures will occur.
Bit reversal interleaving requires that the number of rows be a power of two, so I chose an interleaving order of 128. This implies that each row contains a total delay of 128 bit times divided between transmitter and receiver for an end-to-end interleaving/deinterleaving delay of 16,384 symbols. [7]
The requirement that the signal fit a SSB receiver means that the modulated bandwidth cannot exceed a typical SSB voice filter, usually about 2400 Hz. It should be somewhat narrower to allow for errors in tuning and to stay away from the nonlinear group delay distortion typically found at the edges of crystal filters designed for voice operation where such delay isn't a serious problem.
The Nyquist bandwidth of BPSK is 1 bit/sec/Hz. That is, I could in principle fit 2,000 bits/sec into 2 kHz of a SSB passband while leaving 200 Hz on either side. But achieving 1 bit/sec/Hz with BPSK requires very tight filtering with very little tolerance of symbol timing errors and group delay distortion. The FIR filter used at both transmitter and receiver must be quite long to achieve the necessary response, and processing time in the onboard DSP is limited.
Tightly filtered BPSK also generates a fair bit of overshoot in the RF envelope. This rules out efficient constant-envelope amplification, although that's not a problem in ARISSat-1 because it already gives us a linear amplifier for the entire 2 meter downlink including the telemetry beacon.
So to be conservative, I selected a BPSK symbol rate of only 1 kHz (i.e., 1000 symbols/sec) with a raised-cosine filter having 100% excess bandwidth, i.e., 1/2 bits/sec/Hz. This is achieved with a finite-impulse-response (FIR) filter with 454 taps running at a sample rate of 48 kHz; the same filter taps are used as the matched filter in the demodulator on the ground. Although the resulting bandwidth is still 2 kHz, instead of being flat the signal spectrum rolls off from a peak at the nominal center frequency to nulls at +/- 1 kHz, with relatively little energy near the nulls.
As mentioned in the requirements section, the CW beacon is placed in the lower null of the telemetry beacon spectrum, 1 kHz below the nominal carrier frequency of the BPSK signal. All the operator need do is tune the receiver in USB mode so that the CW beacon comes out at 500 Hz, and this will automatically center the BPSK signal in a typical SSB receiver bandwidth. I.e., the signal will extend from the lower null at 500 Hz to an upper null at 2500 Hz with the carrier at 1500 Hz, the nominal center of the SSB passband.
Fading (or its absence) is also a major consideration in the design of BPSK modems as it can be implemented in two very different ways depending on which channel impairment is more important: thermal (Gaussian) noise or fading.
Satellite links are traditionally designed to minimize thermal noise, so most use a form of PSK that requires the receiver to form a clean local copy of the unmodulated signal carrier to serve as a phase reference for the receive signal. This is coherent demodulation.
This can be done in one of two ways. The first is for the transmitter to send a residual carrier along with the data so that the receiver can track it with a conventional phase lock loop (PLL). The second is for the receiver to reconstruct the carrier entirely from the data by stripping off the modulation.
Although residual carriers are still used in some deep space links, particularly at the extremely low data rates sent by a spacecraft in "safe mode", this takes power away from the data. It is much more common to suppress the carrier entirely at the transmitter so that all of the power can go into the data. The receiver recovers the carrier from the data with one of two mathematically equivalent methods: the squaring loop and the Costas loop.
Especially when strong FEC is used, these loops can suffer significantly from "squaring loss", an effect that reduces the signal-to-noise ratio of the recovered carrier. This happens because the raw symbols (before FEC decoding) are very weak, so when the loop strips off the modulation it does so with a fairly high error rate that degrades the recovered carrier.
Squaring loss can be overcome by merely narrowing the loop filter, effectively averaging out the noise over a longer interval that may span hundreds or even thousands of channel symbols. This is fine if the signal is very stable, as on most deep space links. But it can become completely unworkable when the signal is subject to rapid fading, e.g., on ionospheric or land mobile channels, especially at the low symbol rates we're using here.
We also have fading problems with our low earth orbiting spacecraft. Although we may have continuous line of sight, the spacecraft may tumble unpredictably and sweep antenna nulls past the receiver, causing deep fades accompanied by a sudden reversal of signal phase that would defeat a conventional coherent BPSK demodulator of the Costas or squaring loop type.
For this reason I have chosen a form of BPSK for ARISSat-1 that doesn't require the receiver to form a carrier phase reference. This is DBPSK, differential binary phase shift keying. It is generated just like ordinary BPSK with one crucial exception: before it modulates the transmitter, the data stream is differentially encoded so that a binary zero is transmitted as a 180° change in the phase of the transmitted carrier while a binary one is transmitted as no change from its previous state. This compares with conventional BPSK where a binary zero corresponds to the RF carrier with a 0 degree phase shift and a binary one corresponds to the RF carrier shifted by 180°.
The advantage of DBPSK for our application can be seen in how it is demodulated. The receiver can simply compare adjacent incoming symbols, looking for sudden 180° changes in phase - whatever it may be.
This is extremely easy to implement. In software (the only way to build modems nowadays!), the standard way to demodulate DBPSK is to first convert the input signal to complex baseband at zero frequency. That is, we generate a complex sinusoid (a matching sine and cosine wave) at the estimated signal frequency and multiply it by the input signal (which can be either complex or real) to produce a complex baseband signal at (approximately) zero frequency. If our frequency estimate is correct, an unmodulated carrier becomes a stationary phaser at some arbitrary phase angle (since we don't know or care about its phase). Should the signal flip phase by 180°, this phaser will rotate 180°. By computing the dot product of pairs of complex symbols we simultaneously demodulate the data and remove the differential encoding; this works because the dot product of a vector with itself is a positive number while the dot product of a vector with itself flipped 180° is a negative number.
So instead of generating a nice clean phase reference by averaging some hundreds of symbols, in DBPSK demodulation we just use each symbol as the phase reference for the next. The dot product yields a scalar (a number) that tells us how certain the symbol estimate is, just what we need for our soft-decision Viterbi decoder.
Let's say the BPSK is at a symbol rate of 1 kHz and our frequency estimate is off by 100 Hz. The baseband phaser will rotate 100 times per second, but that's only 1/10 of a rotation (36°) from one symbol to the next. Because the magnitude of the dot product of two vectors is proportional to the cosine of the angle between them, a small frequency error decreases the magnitude of the dot product to cos(36°) = 0.81. This corresponds to a loss of 20*log10(0.81) = -1.84 dB. If the frequency error can be kept to 50 Hz, then the loss is only 20 * log10(cos(18°)) = -0.44 dB, a tolerable figure.
No attempt to acquire data is made at this stage. Only the total demodulated energy is calculated, and the carrier frequency and symbol timing parameters that yield the largest demodulated energy are taken as the best estimates. This step is both CPU intensive and parallelizable, so it's a natural for a machine with multiple CPU cores. But in practice this search is actually pretty fast except on very old and slow machines thanks to a fast FIR filter that uses vector instructions.
Then the data can finally be demodulated.
There are no sync patterns in the BPSK1000 format to indicate interleaver phasing. Correct interleaver phase has to be found by brute force, and this automatically synchronizes the Viterbi decoder phase as well. Once the DBPSK demodulator has acquired and demodulated a symbol stream, the soft decision samples are scaled and fed to 128 virtual deinterleavers, Viterbi decoders and HDLC decoders, one for every possible interleaver phase. Eventually, one of them will produce a HDLC frame with good CRC. Now that we know the correct phasing, the other 127 virtual decoders can be shut down. They remain shut down as long as we continue to get valid HDLC frames. If too much time passes without a valid frame, then all 128 decoders are re-enabled until another frame is decoded.
This was my main motive for using a 32-bit CRC with HDLC; I was concerned that spurious frames would occur frequently with the 16-bit CRC and interfere with the determination of the correct deinterleaver phase.
This brute force approach isn't nearly as bad as it sounds; even when all 128 decoders are running, DBPSK demodulation still takes about half of the program's total CPU time. Demodulation and decoding run in separate threads, both for architectural convenience and to take advantage of extra CPU cores.
This project was very successful, though it was eventually cut short by the complete failure of the spacecraft. I learned a great deal from that experience, and while the ARISSat project has a different set of design objectives and constraints, I was able to reuse many important design elements.
Yet ARISSat-1 will be a very different spacecraft than AO-40, if only because it will operate from LEO while AO-40 was in a high orbit. BPSK1000 is also rather different from my AO-40 FEC design, partly because the latter was constrained to work with the existing Phase III IHU hardware and software: the symbol rate had to be 400 Hz, the modulation had to be BPSK with Manchester (biphase) encoding, the data was fixed-length 256-byte blocks, and so on.
I had none of those constraints with ARISSat-1. In some ways that lack of constraints actually made BPSK1000 more difficult to design, but I think the result is better for it.
Although I've used mostly "off the shelf" modem design elements, as a system BPSK1000 is a new design that has never flown on an amateur radio satellite. I would have liked to implement a range of operating modes, e.g., data rates, bandwidths and interleaver depths, selectable by command so that the optimal mode for the actual conditions could be selected in flight. This wasn't possible so I designed a single mode to be as robust as possible, e.g., by picking a conservatively user low data rate. I very much look forward to seeing it operate from space so we can gain the experience necessary to design improved modems for future flights. With digital signal processing both on the ground and on the spacecraft, and with the new generation of software defined radios, the potential for new amateur satellite digital modes is extremely bright.
[2] For the 32-bit CRC polynomial I chose the one used in Ethernet, sometimes known as CRC-32.
[3] The polynomials and connection vectors for code generator polynomials can be written with either the most or least significant term first, often leading to considerable confusion. The convention here is taken from JPL Deep Space Network Handbook 810-005, 208A, page 12, in which the leftmost bit in the connection vector represents the taps encountered by the newest data bit entering the encoder. Some other references, plus my own software, use the opposite convention. This makes the vectors 1001111 and 1101101 binary; 117 and 155 octal, or 6D and 4F hex.
[4] The interleaver complicates this issue considerably. Even with HDLC bit stuffing (which I use) and alternate FEC symbol inversion (which I don't use) I can conceive of pathological cases where the interleaver might produce a very long string of 1's from a sequence with a bounded number of them. I could have added a scrambler, as I did for AO-40, but with the addition of HDLC bit stuffing I just didn't think the remaining problem was serious enough to warrant it here.
[5] Not to be confused with convolutional coding, which I'm also using here!
[6] As an analogy, consider a group of shuttle busses that run on demand. Each bus carries 50 people, and the drivers like to fill all the seats. If you're part of a group of 50 people who arrive at the bus stop together, you can quickly board the first bus and leave right away. But if 50 people arrive individually over the space of 15 minutes, the first person to board the bus will have to wait 15 minutes for the bus to fill before it leaves.
[7] Strictly speaking the delay should be 127*128 = 16,256 symbols but it the code was easier to write with a little more delay.
[8] Some amateur satellites using BPSK include the Phase 3 series (Phase 3A and Oscar 10, 13 and 40) and the Pacsat series, e.g., Oscar 16.